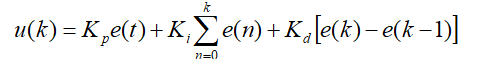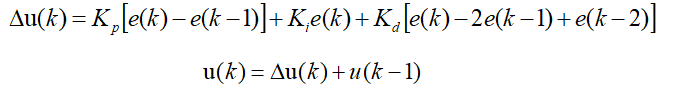2022-01-05 智能车 0 评论

.直立环pd：d参数的引入是为了抑制震荡

p，比例参数，它的作用是反应了控制的响应速度，过小的话平衡车表现是pwm明显不够直立不起来，过大的话小车过于震荡，震荡的时候就要加微分参数抑制震荡·

d，微分参数，它的作用是反应了对震荡的抑制。过小的话和没加微分参数只有比例参数一样的现象，过大的话会低频迅速抖动

控制时序：角度5ms采集一次直立环和角度环10ms控制一次

下面是程序分析：

/************************************************************************/

直立环 ：

int balance(float Angle,float Gyro) { 

float Bias;

int balance;

Bias=Angle-ZHONGZHI; //===求出平衡的角度中值 和机械相关

balance=Bkp*Bias+Gyro*Bkd; //===计算平衡控制的电机PWM PD控制 kp是P系数 kd是D系数 

return balance;

}

角度环pid分析：这里使用的是
位置pid控制器的PD控制器，这里
微分D乘的参数是角速度是因为：这里的角速度已经转变为弧度/s单位，当在单位时间内，车子由一个角度猛然的转到另一个角度的时候，角速度先变大后变为0，这里的角速度就可以理解为在这段时间内的此时的角度差值和上次角度差值的差值(因为角度差值除以单位时间就是角速度)，这就很符合位置pid的微分乘的参数的要求了。所以这里的微分乘的是角速度（这里的角速度单位已经从°/s转为弧度/s）

角度环是根据平衡角度的变化给出的pwm值

kp：是比例参数他决定平衡小车响应速度的快还是慢太小响应速度慢太大会发生低频抖动

kd：是微分参数对于干扰要进行迅速响应的的要加入微分参数太小的话没什么作用太大会高频抖动

只有直立环调试比较好的现象是：平衡车可以直立几秒钟然后像一个方向加速

直立环调试指南：

在调试直立环的时候，我们要把速度环和转向环屏蔽掉，只打开直立环。

（1）先确定平衡车机械平衡位置角度。

（2）确定kp值得极性和大小:

首先我们估计kp的取值范围。我们的PWM设置的是7200代表占空比100%，假如我们设定 kp 值为 720，那么平衡小车在±10°的时候就会满转。根据我们的感性认识，这显然太大了，那我们就可以估计 kp 值在 0~720 之间，首先大概我们给一个值 kp=-200,我们可以观察到，小车往哪边倒，电机会往那边加速让小车到下，就是一个我们不愿看到的正反馈的效果。说明 kp 值的极性反了，接下来我们设定 kp=200,这个时候可以看到平衡小车有直立的趋势，虽然响应太慢，但是，我们可以确定 kp 值极性是正的。具体的数据接下来再仔细调试。

确定 kp 值的大小（令 kd=0，请结合本小节开头的直立控制函数理解）确定参数的原则是：
kp 一直增加，直到出现大幅度的低频抖动。

设定 kp=200,这个时候我们可以看到，小车虽然有平衡的趋势，但是显然响
应太慢了。

设定 kp=350,这个时候我们可以看到，小车虽然有平衡的趋势，而且响应有
所加快，但是响应还是不足以让小车保持平衡。

设定 kp=500,这个时候我们可以看到，小车的响应明显加快，而且来回推动
小车的时候，会有大幅度的低频抖动。说明这个时候 kp 值已经足够大了，需要
增加微分D控制削弱 p 控制，抑制低频抖动(也就是抑制超调)。

（3）确定kd值得极性和大小：

我们得到的 MPU6050 输出的陀螺仪的原始数据，通过观察数据，我们发现最大值不会超过 4 位数（9999），再根据 7200 代表占空比 100%，所以我们估算 kd 值应该在 0~2 之间，我们先设定 kd=-0.5，当我们拿起小车旋转的时候，车轮会反向转动，并没有能够实现
跟随效果。这说明了 kd的极性反了。接下来，我们设定 kd=0.5,这个时候我们可以看到，当我们旋转小车的时候，车轮会同向以相同的速度跟随转动，这说明我们实现了角速度闭环，至此，我们可以确定 kd 的极性是正的。具体的数据接下来再仔细调试。

确定 kd 值的大小（令 kp=500，请结合本小节开头的直立控制函数理解）

确定参数的原则是：
kd 一直增加，直到出现高频抖动。

设定 kd=0.5,这个时候我们可以看到，低频大幅度频抖动已经基本消除。

设定 kd=1,这个时候我们可以看到，整体性能已经非常棒。

设定 kd=1.7,这个时候我们可以看到，小车开始出现高频剧烈抖动(调试过程

遇到这种情况请马上关闭小车，长时间高频抖动会导致驱动被烧坏的)

至此，我们可以确定得到 kp=500,kd=1.7 是 P、D 参数的最大值。然后我们进行最关键的一步，对每个系数乘以 0.6,取整得到 kp=300,kd=1，这就是最终我们需要的参数，这样做的原因是，我们之前得到的参数是 kp、kd 最大值，理想值是根据我们的工程经验，对每个数据乘以 0.6 得到。这个时候我们可以看到，小车没有任何的抖动，非常平稳，但是依然无法保持长时间的直立，直立很短一段时间后会往一个方向加速倒下。这个等我们下面加上速度环才能得到更好的性能。只有直立环是很难让小车达到很好的直立效果的。至此，直立调试部分就告一段落了。

感谢平衡小车之家在技术上的帮助

如果觉得有用的话请关注我哦

也可以和我一起交流，或者评论，我会一一回复。

1.占空比

就是输出的PWM中，高电平保持的时间与该PWM的时钟周期的时间之比。

如，一个PWM的频率是1000Hz，那么它的时钟周期就是1ms，就是1000us，如果高电平出现的时间是200us，那么低电平的时间肯定是800us，那么占空比就是200：1000，也就是说PWM的占空比就是1:5。

2.分辨率

也就是占空比最小能达到多少，如8位的PWM，理论的分辨率就是1：255(单斜率)，16位的的PWM理论就是1:65535(单斜率)。

频率就是这样的，如16位的PWM，它的分辨率达到了1:65535，要达到这个分辨率，T/C就必须从0计数到65535才能达到，如果计数从0计到80之后又从0开始计到80…，那么它的分辨率最小就是1:80了，但是，它也快了，也就是说PWM的输出频率高了。

3.双斜率 / 单斜率

假设一个PWM从0计数到80，之后又从0计数到80… 这个就是单斜率
假设一个PWM从0计数到80，之后是从80计数到0… 这个就是双斜率

可见，双斜率的计数时间多了一倍，所以输出的PWM频率就慢了一半，但是分辨率却是1：(80+80)=1:160，就是提高了一倍。

假设PWM是单斜率，设定最高计数是80，我们再设定一个比较值是10，那么T/C从0计数到10时(这时计数器还是一直往上计数，直到计数到设定值80)，单片机就会根据你的设定，控制某个IO口在这个时候是输出1还是输出0还是端口取反，这样，就是PWM的最基本的原理了。

传感器（陀螺仪和加速度计）

(4条消息) 陀螺仪原理–转载_jaczen的博客-CSDN博客_陀螺仪原理

- 加速度计（accelerometer）检测什么

- 陀螺仪（gyroscope，也称作 gyro）检测什么

- 如何将传感器ADC读取的数据转换为物理单位（加速度传感器的单位是g，陀螺仪的单位是度/秒）

- 如何结合加速度传感器和陀螺仪的数据以得到设备和地平面之间的倾角的准确信息

加速度计检测到得力的方向与它本身加速度的方向是相反的。这种力量通常被称为惯性力或假想力

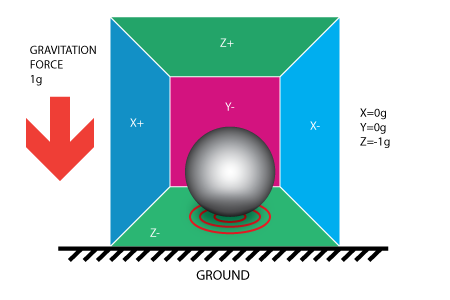
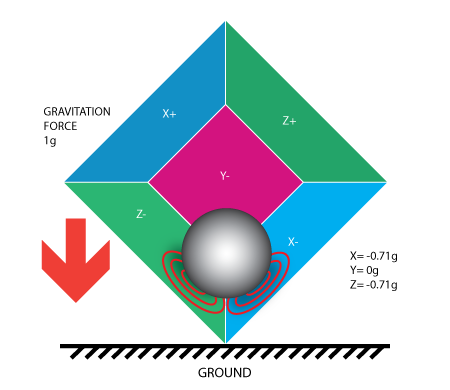
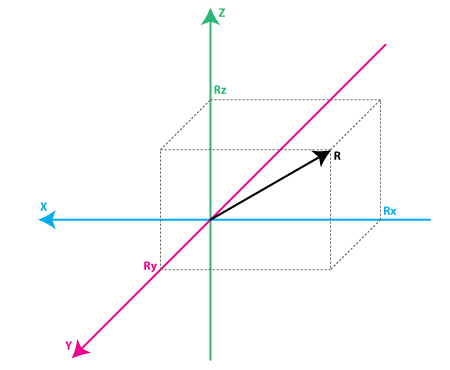
R ^ 2 = RX ^ 2 + RY ^ 2 + RZ ^ 2（公式1），此公式等价于三维空间勾股定理。

直立车，PID部分

角度环

(4条消息) 【平衡小车制作】（五）位置式PID、直立环与速度环概念（超详解）_鲁乎乎的博客-CSDN博客_直立环

这个信息挺全的

直立平衡角度环PID控制 · 给新手的两轮自平衡小车开发实战指南 (miaowlabs.com)

PID

(4条消息) PID应用时要注意的一些点_maitd的博客-CSDN博客_pid限幅

位置式连续式

这里写图片描述

位置式离散式(注意此时Kp=Kp, Ki=Kp*T/Ti, Kd=Kp*Td/T)

在这里插入图片描述

增量式离散式：

在这里插入图片描述

参数整定找最佳，从小到大顺序查 
先是比例后积分，最后再把微分加 
曲线振荡很频繁，比例度盘要放大(Kp减小) 
曲线漂浮绕大湾，比例度盘往小扳(Kp增大)
曲线偏离回复慢，积分时间往下降(Ki增大)
曲线波动周期长，积分时间再加长(Ki减小)
曲线振荡频率快，先把微分降下来(Kd增大) 
动差大来波动慢。微分时间应加长(Kd减小) 
理想曲线两个波，前高后低4比1 
一看二调多分析，调节质量不会低

二.控制PID的执行周期(T)
虽然在离散化的公式里这个地方这个参数隐藏了,但注意它只是被隐藏了,但还是还会发生作用,看一下离散位置PID公式里那几个参数的公式,是不是它会影响参数的大小啊.
所以在应用第二个第三个PID公式时执行周期一定是要确定的,不能变更的,一T变更那么参数就得跟着变了,注意是T变了,参数就得相应的去变化,而不是一直不变,但如果此时你的参数维持不变的话,显然这组参数已经不是当前的最优参数了.
举个例子,有一个取样周期为1的PID和一个取样周期为10的PID控制同一个的执行元件,若此时参数还采取一样,它的控制效果显而易见是不会一样的.所以要控制执行周期,最好能将Ki=KpT/Ti, Kd=KpTd/T,这个公式直接应用,公式变为:
这里写图片描述

我推荐用这个公式,在控制好T,或者获取T的实际值,代入,调节Ti和Td.许多开源四轴的控制一般是用这个公式的.

三.积分环节的限幅
我不推荐做智能车啥的用增量式PID,说是简化了运算,但现在的单片机啥的运算能力和频率都挺强的,又不是51那个时代了,所以减那一点实在没什么作用.此外用增量式PID,不好去做积分限幅的,只能对每次的输出做限制,但对积分的限幅没什么作用.
有时候当误差量e(k)比较大,而e(k)-e(k-1)要小的多的时候,系统有较大的迟滞的时候(感觉是)要防止积分的饱和.就是当系统的输出一直摇摆,不会收敛,而且摇摆的频率比较缓慢,那么我感觉可能是饱和,得限制下积分了.也就是

这个环节的累积值大小做限幅.
我感觉用的时候可以最后加积分环节,看一下系统的稳态误差,如果没稳态误差,我就直接不加了,如果有的话,那么看一下稳态误差的大小在什么范围,积分限幅也就大致限制在那个范围了.

四.微分环节的滤波
当系统容易收到高频信号的干扰时,微分作用会将高频信号的扰动放大(自控课本上说的),高频信号变化的较快,而微分是去求误差的变化率,所以有高频扰动信号,就会被微分作用给放大,建议对微分环节做低通滤波,通常是一阶低通滤波,讲低通滤波的帖子文章挺多的,我就不写了.

五.关于各种自适应PID
包括什么神经网络PID,模糊PID,遗传算法优化PID等等,本质上都是对参数的统计和优化,但通常这些算法运算量时挺大的,写肯定可以写出来,但这个在一些嵌入式设备上运行的效率速度不是很好,会占很大的运行速度,而且要搞清楚各种自适应PID的使用范围,比如模糊PID适用于过程控制,控制个温度什么的,它不适合用来做运动控制,控制电机什么的,因为计算量较大,在单片机上还有可能会参数迟滞什么的.做个智能车类的小东西,还是用不上这些方法的,单纯PID就够了,论文里的一些自适应PID方法,不一定都是经过实际检验的,可能只是在MATLAB里做了个仿真.所以我感觉不能全信.

先把单片机，驱动芯片，陀螺仪，加速度计，电机准备好。

然后搭车，质量尽可能集中在两个车轮轴心线，陀螺仪和加速度计也要尽可能放在轴心线。

我这个是个错误的示范，质量比较分散了，但是又无可奈何，又想要零点，又想把传感器伸的远一点。。。

然后调试代码，1读取三轴加速度和角速度2姿态结算，互补滤波，四元数，卡尔曼估计器都可以。

直立控制，找出你的车的机械零点，也就是质量平衡点。最简单的方法：电机输出=p*（当前角度-期望角度）＋d*（角速度）

参数整定参考一下csdn的一些文吧。

你的车就立起来了。

直立控制不止这一种，也有各种双pi，双pd的串级控制等等。

然后再搞速度和方向。

可以去智能车论坛找个代码研究一下。

https://www.its203.com/article/Mark197/119486864?2022-03-13T1?2022-03-20T0

图1.串级PID流程框图

机械结构的设计决定了整个系统的极限，硬件电路提供实现极限的方法与条件，而软件算法则是决定了整体系统能否达到极限

https://www.its203.com/article/Mark197/119486864?2022-03-13T1

直立车模控制中三种滤波算法简单分析

https://www.eefocus.com/sensor/467379?_ga=2.136496885.490729479.1647172634-1494707267.1647172610&pk_vid=3f99cf4edfd158d71647182427d8fba1

参数调试的话可以参照平衡小车之家的平衡车调试指南来进行相应的调试，里边写的还是比较好的哦https://wenku.baidu.com/view/3e5fc765bb4cf7ec4bfed00b.html

这里说一下机械结构对控制的影响。机械结构对直立控制的影响还是比较巨大的，特别是车速越快对结构的要求就越高，如果只是单纯的想立起来的话对结构的要求则没那么高。

主要遵循的原则就是机械重心越集中、越靠近两车轮轴线越好。车子除去底盘的话基本就电池和电路板了。电池是比较重的，所以可以优先考虑电池的放置，其次就是考虑电路板的放置了。重心越低越靠近车轮轴线相应的PID参数的调试就会更加的简单。反之的话则会更难。

https://www.cxy80.com/article/qq_36240874/100026227

https://its401.com/article/qq_46336588/119916341

关于直立环

https://www.guyuehome.com/24372

详细介绍如何从0开始写一个数据通信，将数据从单片机发送到上位机（或者虚拟示波器）进行数据或图像显示，以及常见问题或注意事项解答 https://www.guyuehome.com/19990

卡尔曼滤波（非矩阵）在平衡直立车直立角度测量中的应用（MATLAB模拟仿真），简单易懂，详细注释，附卡尔曼滤波(矩阵) https://blog.csdn.net/qq_44339029/article/details/105597930

直立车的控制可分为直立环、转向环、和速度环，首先要写的肯定是直立环，直立环根据姿态传感器的数据，进行直立环PID控制，输出直立环PWM，使车保持直立状态，直立车直立是基础，当然直立环也不是越硬越好，这个看个人的需要吧，关于直立的角度，经过我的多次实验，一定不要太低，过低后会带来很多不必要的麻烦（比如上坡道时车不稳，贴地，电感值异常等），一般直立环调节到原地站立在机械零点，给予下压或者上挑干扰后可以在短距离的前后移动后恢复稳定状态，这时候就可以加转向环了，之前刚开始调完直立环后，我直接加的速度环，发现虽然给两个电机相同的PWM值，但是我的车就是不跑直线，后来经过数据采集后发现，两者的转速也没有什么规律可言，通过差值PWM来使其走直线也是不可行的，索性就直接先加转向环，通过转向环的作用来纠正其偏离中心赛道的偏差，发现效果很好，调完转向环后再调速度环（同时调也行），转向环和速度环都可以看做是对直立环的干扰，推荐使用串级PID的方法

直立环：在周期性中断中采集姿态传感器的数据，比如10ms采集一次，在主函数中初始化相应的外设，比如姿态传感器MPU6050的初始化、IIC的初始化、电机PWM的初始化，然后在直立控制函数中，先调用写好的由陀螺仪和加速计计算角度的函数，分别计算出当前小车距离地面的夹角，然后采用滤波算法，获取其融合后真正使用的角度值，然后将该角度值与设定的机械零点值相减，获取偏差通过PID算法对其进行控制，调试参数使其保持直立

转向环和速度环：在周期性中断中采集电感值ADC的数据，比如10ms采集一次，在主函数中初始化相应的外设，比如编码器所用的定时器的初始化、电感值ADC通道的初始化等，然后在控制函数里，读取编码器的值，并对其进行异常数据检查及处理，适当的滤波处理，然后由左右编码器的值得到车中心的速度值与设定值做差来获取速度偏差进行控制，在输出速度环和转向环PWM时建议采用平滑输出的方式，来减小短时间内对直立环的干扰，此外关于转向环，根据在不同的赛道元素采用不同的转向环系数的方式来增强控制效果，当然这种方法虽然使得控制效果更优化，但是需要检测和判断赛道元素，调试的参数也变多了，大家根据实际情况选择是否使用，还有非常重要的一点各环PWM的输出一定要限幅，限幅值的大小也是很重要的调节参数，尤其是直立环的

MCU（Microcontroller Unit）微控制单元，核心板上的芯片

USB转TTL是可以直接转换，插头同时插在塑料壳上的

编码器分正交编码器和角度编码器(不用了)，一个是带方向的(数字显示正负表示正反)，一个不带方向 512

速度环、直立环、转向环

电子设计竞赛(4)-常用的两种PID算法 (qq.com)

基于TC264的两种电机驱动使用教程及PID算法浅析–逐飞科技 (qq.com)

陀螺仪：灵敏度高，调整舵机角度偏转

(33条消息) 平衡车直立PID调节总结_a568713197的博客-CSDN博客_平衡车pid

这个有代码参考

(33条消息) PID实践笔记-PID浅解及两轮直立车参数调试经验_尔过留香的博客-CSDN博客_方向环pid

这个很不错

(33条消息) PID实践笔记-两轮直立车的速度控制_尔过留香的博客-CSDN博客_直立车速度环

拒绝瞎调，用matlab，自动调节PID参数 - 知乎 (zhihu.com)

好方法！！

[平衡小车PID，就该这么调！！！ - 知乎 (zhihu.com)](https://zhuanlan.zhihu.com/p/119160742#:~:text=在直立环中，PID的入口参数为：平衡小车的姿态角和姿态角对应的角速度。,值得说明，MPU6050得出来的姿态角有三种：PITCH（俯仰角）、ROLL（翻滚角）、YAW（航向角）一般来说，MPU6050都是平方且平行装在平衡小车上，总不会有人垂直装吧。)

调参

(1条消息) 直立车想节能——2020全国大学生智能车车竞赛经验记录之我想要直立（平衡小车串级pid调参经验）_沉睡的小灰的博客-CSDN博客_平衡车串级pid

平衡车我相信很多电赛测控的入门的玩家都也玩过，很多朋友们也都听说过平衡小车之家这家淘宝店铺。而串级PID也是一个经典且牛批的方案而广为人知，所以在这样的比赛结束之后作为俩套方案都试过的我，谈一谈平衡小车之家的代码即并行的pid和串级pid的优缺点以及调参经验。

三环介绍
废话少说正题开始

我相信大家都应该很了解PID是什么，以及 P I D分别是干什么的，这里就不详细介绍了。反而我想谈一谈平衡小车的控制需要什么。

首先我觉得大家更为熟知的是角度环，速度环，和转向环。角度环是为了控制小车的一个直立，速度环是为了控制小车的速度，而方向环则是为了控制小车的转向。其实这三个环分别起到什么作用是非常好理解的。

角度环也叫直立环，就是机械中值的角度值为目标值，误差为目标值减去当前姿态传感器读到的角度即
误差角度 = 中值角度 - 当前角度

速度环，就是你设定速度为目标速度，如果想他站着不动，那么设定的目标速度就是0，误差就是编码器读到的车轮的值，如果是俩个车轮就将其加起来乘或不乘一个1/2（本质没区别）。
误差速度 = 设定速度 - （编码器左+编码器右）

转向环，转向环通过读取航向角的角速度来，其实本质上还是控制这个角速度为莫个值。比如你想小车走直线，那么你就需要设定值为0，误差值就是设定值减去角速度
误差转向 = 设定转向 - 航向角角速度

那么并行pid和串级pid有什么区别呢？

并行PID
如何做
并行的PID是将三个环分别独立计算，最后叠加起来最后输出到电机上面去即
电机PWM = 直立环 + 速度环
如果加上转向环就是

电机左PWM = 直立环 + 速度环 +（转向环/2）
电机左PWM = 直立环 + 速度环 - （转向环/2）
（加减得看你的极性）

为什么这样做
其实这三个环分别都很好理解，直立环控制直立，速度环控制你的速度，转向环控制你的转向。
至于为什么叠加起来就能直接赋值给电机好像是可以参考卓大大之前的那片文章，里面有对模型的详细介绍。

这样做有什么好处
其实并行pid最大的好处就是现象十分明显，为什么这么说呢？
直立环加上你就能看见小车能立起来了，速度环加上你就能看到小车停止或者按照指定的样子跑，转向环也是这样，你能看到小车转向很明显。明显带来的效果就是非常方便你调试PID你可以很清楚的看到现象，从而PID的参数整定就会十分顺利。由于参数调试十分简单这里就不详细介绍了，在很多淘宝店铺都提供了很多代码，包括b站也都有许多教程。

串级PID
因为串级pid有很多种串联的方法，我在这里仅介绍一下我的方法，和按照我的方法的效果，仅供参考

如何做
串级pid不同于上面的，会多出一个环叫做角速度环，而且串级pid会多出一些概念，如内环和外环。我的串级pid的构造为，角速度内环，速度外环，中间是角度环，叠加转向环。具体是怎么工作的呢？
速度环的输出结果作为角度环的设定值，角度环的输出结果作为角速度环的设定值，角速度环的输出结果累加上我们上面介绍的转向环作为我们的电机PWM的输出。

速度环——>角度环——>角速度——>输出 + 转向环 = PWM

为什么这样做
首先两点，多出了一个串起来和一个角速度环。

汉堡告诉我的是，串起来的目的是为了PID更快的收敛，但是我个人的感觉不止于此。我认为串级PID能给传感器很多信息分布不同的权重，并且让其有序，而不是简单粗暴的累加起来，就像煮大锅饭一样。

角速度环是我一开始最不能理解的一个东西，我队友也十分抗拒加上这个东西，可是我到最后才发现角速度环才是这个串级PID的灵魂。如果大家调试过直立环大家就会发现一个问题就是，如果直立环调的太软（p比较小）你会发现整个平衡小车会有点来回的低频振荡不能稳住，如果你的调的太硬（p比较大）你会发现整个车会在高频抖动，这种情况下一是容易烧电机驱动（来回转电流很大都是堵转电流，不要问我为什么知道容易烧，我板子经历了他这个年纪不改经历的惨痛），二是你会发现车非常抖，就包括你加上速度环之后，你的车在行进过程中十分抖动，这会非常耗电，对节能就不友好了，而且车子是不稳定的（太软车就容易倒，甚至一碰就倒）。你要调试到那种堪堪不抖动，而且车还不容易倒的状态下，这个pid的参数十分难调，而角速度环就能解决这个问题。我在调试之前问学长，角速度环的目的是干什么的，他给我的解答是能排除扰动和干扰。我一开始一直认为排除的扰动可能是车在进行过程中装到旁边的路障，或者转向过大的时候带来的不稳定，可是我到最终发现其实角速度环能解决的一个很大问题的就是你直立环调的过硬的时候，所带来的高频抖动，角速度环能帮助你去掉这个高频抖动。所以从这一点来说，你的角速度环和速度环调的得较为适配，这样你的车很难倒下，而且车不会很抖。

这样做有什么好处
我在上一点上也大概说了串级pid的几点好处，首先你会直观的发现你的车非常非常非常稳，稳到什么地步呢，基本上你的电磁前瞻杆子你拍一下他能起来而且不会倒，我在侧面对着车踢一脚车也是不会倒的。其次你的加速会非常明显只要你的重心不要过分的往后，加速是很到位的。最后就是避免了高频抖动，避免了电机的堵转，也会进一步节能。

缺点也很明显
其实带来好处的同时就会带来缺点，缺点就是PID十分难调，因为你的pid是一环套一环，首先你出了问题，现象不容易看出来是哪个环的问题，主要是角速度环和角度环，然后就是怎么调整，而且中间某个环的参数没调好，后面的都不好使，这就带来了很多挑战和难题。

我该怎么调
在串级pid中，内环是直接输出的，对于这一点来说，外环粗调就ok，内环精调。对于我们这个模型来说，主调角度环副调角速度环，调参顺序是从内环到外环，最后调转向环。
首先调参角速度环，角速度环一般是pi控制，其实很多地方有用增量式也有用位置式，对于内环的角速度环，我们需要高频控制，大概每2ms运算一次，对于这样的运算我们可以选择增量式来减少我们的运算量，当然对于增量式不熟用位置式也是一样的。在调整这个参数的时候与以往不同，我们需要先调整i的参数，原因是陀螺仪的角速度跳动非常大，十分容易出现静差，我们需要加上i来消除那部分静差，调整的现象是加上i车就能大幅的低频来回晃，能勉强立住，立住的效果越好i的参数越好，i过大也会导致高频抖动。在调整完i的参数之后我们就需要调p的参数，其实加上p之后你会发现车就能勉强立住了，不会晃的很大，你需要增大p大概到车子会稍微抖动，还没要到高频抖动的感觉。效果就是小车基本上能立起来。
其次调角度环，角度环一般是pd控制，大概是10ms运算一次（串级pid 的级和级之间的运算时间是2-9倍之间），加上角度环的p之后你会发现小车基本上能稳稳的立住了，当然这是合适的p，但是区分这个的现象真的一点都不明显，我的方法是拍前瞻的杆子，看响应速度，力气越大响应速度越快，说明效果越好，其实基本上车是会往前冲，来调整角度，你也可以看冲完之后小车稳定下来的pid收敛速度，来判断p的值是否合适。基本上p感觉调到差不多了的时候，可以加上d，d是提高车的响应速度，加上d之后你会发现小车向前冲的距离会不大，力气不大的时候，能看到小车立刻弹起来，这就是比较好的响应速度，d过大也会带来高频的抖动。加上合适pd之后你会发现小车基本是很稳定的立在地面上，除非特别暴力什么的，小车是不会倒的，哪怕是撞上什么物体，或者是碾过什么物体都不会倒。**这个角度环得调的比较硬，这样你才能在加速的时候看起来效果比较好，不然你会看到小车在形式过车中，车身比较抖或者车容易倒，这是俩个极端。**角度环是比较重要的一个环，需要我们耐心去调试。其实这也会面临一个问题，我大概调到什么样子才能到下一个环上面去调，这就得靠自己的尝试和感觉了，我个人觉得需要自己多调一调就会找到那个感觉，我调了三遍，第一遍调了大概五六个小时，第二遍调了大概2-3小时，第三遍一个小时就调完了，需要自己摸索找感觉。
最后速度环，速度环的调试其实比较粗糙了，感觉速度环的p就是小车的一个加速度，p越大加速度越大，甚至速度环不加i都是可以的。虽然速度环的i固然会积分导致一些问题出现，但是我们可以用多少次的一个清零尽可能的解决这个问题，**如果不加i的话，感觉速度会不稳定，**这就对你的直立环和角速度环提出了很大的考验，我看到的一个朋友就是没有加i，我看他加速的时候车屁股一直在点地，虽然规则是允许平衡车的第三点点地，但是这比如对我们的节能产生了很大的影响，节能的很重要的一个前提就是稳定的工作，以我们的电瓶车为例，频繁的加速减速你车的待电就不行。
转向环其实都是差不多的，但是有一点就是转向环需要和速度形成一定的联系，因为转向的多少是累加在我们角速度环的输出上，和并行那边是差不多的，如果你转向环是死的，你高速和低速状态下的转向环的值不一样，这就容易出问题。我看到人家的代码是利用一个俩个的串级串到一起，是利用电磁的差比和作为当前值，设定值为0，进一个pid算出参数，当前的航向角的角速度为当前值，这个参数乘上速度作第二个pid的设定值，第一个pid还是一个动态pid，感觉挺巧妙的，由于时间关系没有尝试

在这里插入图片描述

END
调参很苦，熟能生巧，思考现象，方能直立
感觉踩了很多坑，也问了很多人，非常感谢这一路上许多学长耐心解答，我也希望我的文章能给别人带来一丝丝参考价值。节能直立挺好玩的，但是很可惜，在方向上走错了很多，只能怪我太菜了。愿大家都能做出三米神车，越来越牛批！

突然有些朋友问我要代码，其实我也没什么可以给的，pid都是一个样子，可以给大家看一下流程的样子(这是学长的代码)

void Balance_Control(void)
{
	if (Ang_Velocity_Flag)	// 直立角速度环	2ms
	{
		Ang_Velocity_Flag = 0;
		ICM_GetData(&GYRO,&ACC);
                //Data_Filter();//原始数据滤波
                Data_steepest(); 
                 IMU_update(0.008f,&(sensor.Gyro_deg), &(sensor.Acc_mmss),&imu_data); //匿名移植姿态解算
                icm_gyro_z = LPButterworth(icm_gyro_z, &Gyro_Butter, &Butter_20HZ_Parameter_Acce);//巴特沃斯30HZ滤波    Z轴和Y轴角速度都用原始数据，只经过滑动滤波和低通处理
                icm_gyro_y = LPButterworth(icm_gyro_y, &Gyro_Butter1, &Butter_30HZ_Parameter_Acce);
                //IMUupdate(GYRO.X*Gyro_Gr, GYRO.Y*Gyro_Gr, GYRO.Y*Gyro_Gr, ACC.X*AcceRatio, ACC.Y*AcceRatio, ACC.Z*AcceRatio);
                state = Long_street();
//                if (state)//障碍，长直道减速
//                {
//                  Speed_Set = 180;
//                }
//
//                else
//                {
//                  Speed_Set = 320;
//                
//                }
               //Middle_Err = LPButterworth(Middle_Err, &Middle_Err_Butter, &Butter_10HZ_Parameter_Acce); 
		Radius = -PlacePID_Control(&Turn_PID, Turn[Fre], Middle_Err, 0);//动态PID，动态范围0-0.04	，大误差时起作用，
                
		Theory_Duty += -PID_Increase(&Ang_gyro_PID, Ang_gyro, (int32)icm_gyro_y, (int32)(Tar_Ang_Vel.Y));										/* 角速度环作为最内环控制直立 */
		//abs +=PID_Increase(&Ang_gyro_PID, Ang_gyro, (int32)(GYRO_Real.Y*10), 0)*10;//(int32)(Tar_Ang_Vel.Y));	// 计算直立PWM
                //abs +=Theory_Duty;
                //Theory_Duty += Theory_Duty;
                //Theory_Duty = -Theory_Duty;
               //abs = abs * 10;
		Theory_Duty = LIMIT(Theory_Duty, -900, 900);
                //Direct_Parameter = -PID_Realize(&Turn_gyro_PID, Turn_gyro, (int32)(icm_gyro_z),0);
                Direct_Parameter = -PID_Realize(&Turn_gyro_PID, Turn_gyro, (int32)(icm_gyro_z),Radius*Speed_Min);	// 转向环左正右负
                Direct_Parameter = range_protect(Direct_Parameter, -800, 800);
		Direct_Parameter = Turn_Out_Filter(Direct_Parameter);//输出滤波
		
//		Direct_Parameter = Direct_Last*0.2 + Direct_Parameter * 0.8;	// 更新上次角速度环结果	
//                Direct_Last = Direct_Parameter;
		//Direct_Parameter = 0;
		MOTOR_Duty_Left  = Theory_Duty + Direct_Parameter;	// 左右电机根据转向系数调整差速
		MOTOR_Duty_Right = Theory_Duty - Direct_Parameter;	
		
		//get_angle();
               // Kalman_Filter(Mpu_date.roll, Mpu_date.groy);//卡尔曼滤波

                
               
	}
        if (AngleJS_Flag)
        {
          AngleJS_Flag = 0;
         
        }
	
	if (Angle_Flag)		// 直立角度环	10ms
	{
		Angle_Flag = 0;
		
		get_speed(&left_speed,&right_speed);// 获取当前速度
                //speed_measure(left_speed, right_speed);
		Speed_Now = (  left_speed-right_speed)/ 2;
                Distance = Speed_Now + Distance;
		Speed_Now = Speed_Now * 0.8 + Speed_Last * 0.2;
                Speed_Last = Speed_Now;
                //Long_Load();
                Tar_Ang_Vel.Y = -PID_Realize(&Angle_PID, Angle, (int32)(imu_data.pit*100), (int32)Target_Angle.Y);	
		Tar_Ang_Vel.Y = range_protect(Tar_Ang_Vel.Y, -1000, 1000);	// 注意正负号
 
                
                
	}
	if (Speed_Flag)		// 速度环	50ms
	{
		Speed_Flag = 0;
												/* 速度环加到角度环上串级控制 */
		Target_Angle.Y = -PID_Realize(&Speed_PID, Speed, Speed_Now, Tar_v+Speed_Set);	// 结果为放大1+00倍的目标角度
		Target_Angle.Y += Zero_Angle*100;	// 目标角度叠加在零点上
                //Target_Angle.Y = -Target_Angle.Y;
//                if (Middle_Err>=500 || Middle_Err<=-500)//一定程度上防止弯道减速
//                {
//                  Target_Angle.Y = 3500;
//                }
		Target_Angle.Y = range_protect((int32)Target_Angle.Y, 200, 3000);

		Speed_Min = Speed_Min * 0.1 + Speed_Now * 0.9;
		if (Speed_Min < 40)
		{
			Speed_Min = 40;
		}
                
                //oled_int16(84,0,Target_Angle.Y);
	}
        
}

以及位置式pid的代码

// 位置式动态PID控制
int32 PlacePID_Control(PID *sprt, float *PID, float NowPiont, float SetPoint)
{
	//定义为寄存器变量，只能用于整型和字符型变量，提高运算速度
	float iError;	//当前误差
	int  Actual;	//最后得出的实际输出值
	float Kp;		//动态P
	

	iError = SetPoint - NowPiont;	//计算当前误差
	sprt->SumError += iError*0.01;
	if (sprt->SumError >= PID[KT])
	{
		sprt->SumError = PID[KT];
	}
	else if (sprt->SumError <= PID[KT])
	{
		sprt->SumError = -PID[KT];
	}
	//二次函数是为了达到 误差越大  反应越快 回复力越大 其中 KI值是误差为0时的P 也就是直道上的P值
	Kp = 1.0 * (iError*iError) / PID[KP] + PID[KI];	//P值与差值成二次函数关系，此处P和I不是PID参数，而是动态PID参数，要注意！！！
	
	Actual = Kp * iError
		   + PID[KD] * ((0.8*iError + 0.2*sprt->LastError) - sprt->LastError);//不完全微分  
	sprt->LastError = iError;		//更新上次误差
	
	Actual = range_protect(Actual, -260, 260);
	
	return Actual;

}

本文链接： https://zhang0224gz.github.io/2022/01/05/智能车/PID/

版权声明： 本博客所有文章除特别声明外，均采用 CC BY 4.0 CN协议许可协议。转载请注明出处！

Eureka

Study Notes & Supplement

传感器（陀螺仪和加速度计）

直立车，PID部分

角度环

PID

调参

EurekaStudy Notes & Supplement