最优化方法广泛应用于工农业、交通运输业、商业、国防、建筑、通信与政府机关及管理各部门各领域,旨在解决最优计划、最优分配、最优决策、最佳管理等最优化问题。最优化方法是一门应用科学,它以量化为基础,融合多学科交叉特点,强调做出最优决策
内容包括线性规划、运输问题、整数规划、非线性规划的基本概念与基本原理、无约束问题的最优化方法和约束问题的最优化方法
线性规划问题
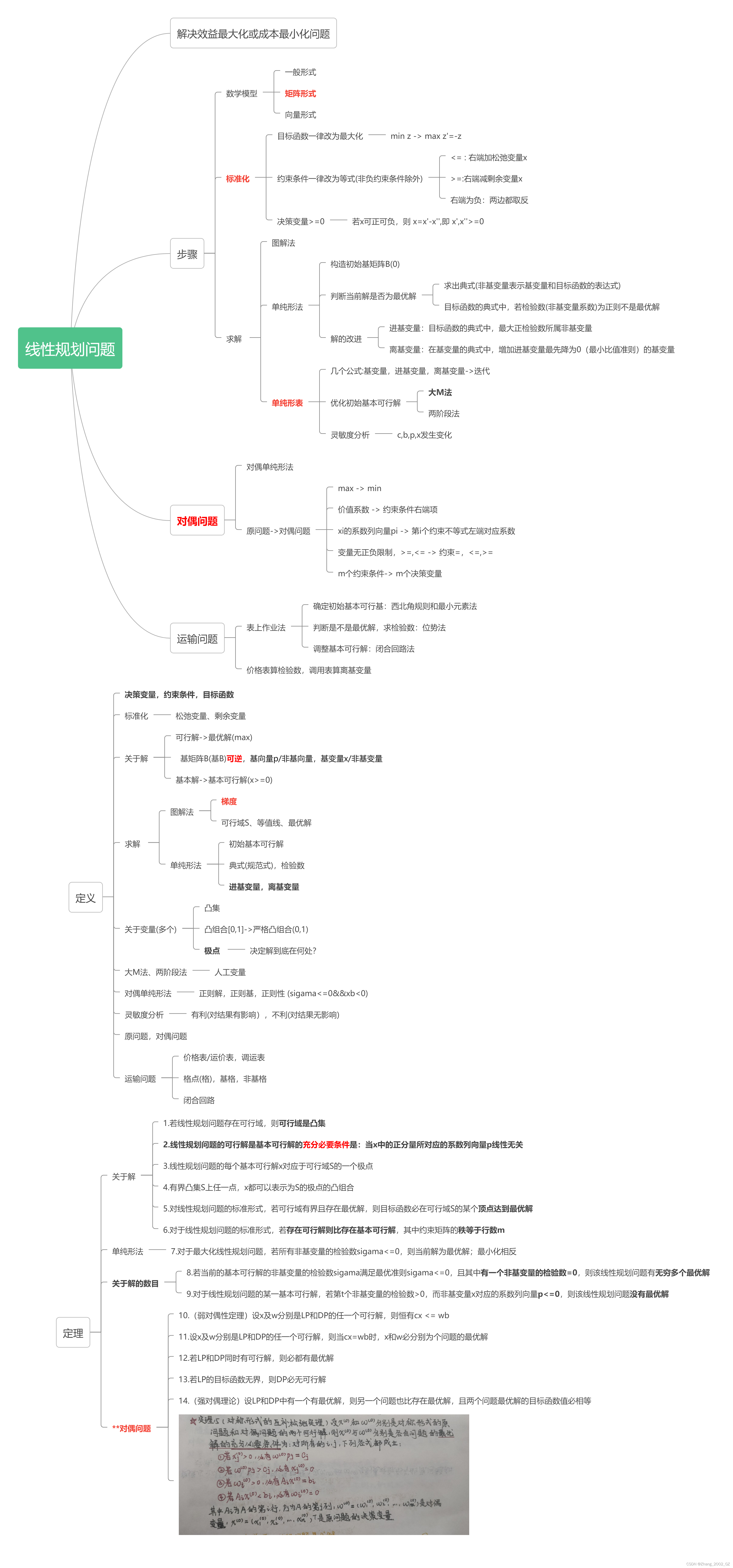
我们将一个问题抽象为在满足一组约束条件下,寻求变量x1,x2…xn使目标函数达到最大值的一个数学问题


线性规划数学模型

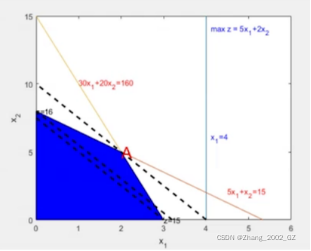
->可行域:满足约束条件和非负条件的点组成的交集
->最优解:



线性规划标准形式
目标函数一律改为最大化
约束条件一律改为等式(非负约束条件除外)
等式右端项大于等于零
-> 两种形式:一般形式、矩阵形式和向量形式



-> 将非标准形式化为标准形式



例子:




