1.1 信息安全与密码技术
信息安全是目的,密码技术是解决方法
1.2 密码技术发展简介
古典密码时期
时间:古代–19世纪末
人工,未形成学科,仅能称其为密码术
近代密码时期
时间:20世纪初–20世纪50年代左右
自动编码的转轮密码机:德国“艾尼格玛”ENIGMA密码机
现代密码时期
时间:1949年–现在
香农的奠基性论文“保密系统的通信理论”
1.3 密码学基本概念
密码学的主要任务
- 机密性:非授权用户不得访问
- 数据完整性:不允许添加,删除,篡改等
- 鉴别:消息的来源和本身的真实性
- 抗抵赖性:已发(先前的通信行为及其相关内容)不可以否认
密码学两方面:密码编码学和密码分析学
密码体制的五大部分
- 消息空间M,即明文空间
- 密文空间C
- 密钥空间K:加密秘钥和解密秘钥
- 加密算法E
- 解密算法D
啥啥空间:一个非常大的数据集合
熵:衡量信息的不确定性
max:等概率例子:算法 Y=aX+b, 秘钥 a,b E(m)=c -> 秘钥,即 f
密码系统的安全性
密码攻击者常用方法
- 穷举(暴力攻击)
- 统计分析 --> 规律
- 数学分析攻击 --> 数学模型
| 攻击类型 | 攻击者拥有的资源 |
|---|---|
| 惟密文攻击 | 加密算法 截获的部分密文 |
| 已知明文攻击 | 加密算法 截获的部分密文,和相应的明文 |
| 选择明文攻击 | 加密算法 截获的部分密文;加密黑盒子,可加密任意明文得到相应的密文 |
| 选择密文攻击 | 加密算法 截获的部分密文;解密黑盒子,可解密任意密文得到相应的明文 |
当前密码算法只要抵抗住穷举攻击状态下,惟密文攻击的攻击就是成功的
密码算法要求
- 数据复杂性:计算量
- 处理复杂性:花费时间
- 存储复杂性:空间大小
密码算法安全性的因素
- 密码算法的保密程度
- 之外的不安全因素(管理程度)
密码算法的保密强度并不等价于密码系统整体的安全性。一个密码系统必须同时具备完善的技术和管理要求,才能保证整个密码系统的安全。
密码系统的安全性
-
无条件安全性
一次一密,秘钥不能重复使用 --> 存储管理花费巨大,不采取
-
可证明安全性
数学难题:大整数素因子分解,计算离散对数(log n = b%m,模前可能b无穷等于余数) --> 解决耗费时间过大
-
计算安全性性
当密码系统的秘钥空间足够大时,由于攻击者受计算条件、资源限制,而且有其特定目的,若不能在希望的时间内或实际可能的条件下破译成功,则称计算上不可破译
达到实际安全性要满足的准则
- 实际计算量十分巨大
- 计算时间超过被加密信息有用的生命周期
- 破译该密码系统的费用超过被加密信息本身的价值
1.4 密码系统设计的基本原则
科克霍夫斯(Kerckhoffs)原则
数据安全基于秘钥而不是算法的保密性
- 密码设计公开原则并不等于所有的密码在应用时都一定要公开密码算法
1.5 密码体制的分类
按秘钥数量
| 对称密码体制 | 非对称密码体制 |
|---|---|
| 也称单钥、秘密密钥…… | 也称双钥、公开密钥…… |
| c=Ek(m), m=Dk© | c=Epk(m), m=Dsk© |
| DES(56 bits) --> AES(128 bits) | RSA --> ECC |
| O(n2) : C(2,n) = n(n-1)/2 | O(2n): 每人分配一个公钥一个密钥 |
| 加/解密使用一样,效率高 密钥管理成本高,麻烦(比如分发) |
加/解密使用不一样,效率低 密钥管理简单 |
| 公钥不可解出密钥,密钥可以推出公钥 |
根据对明文信息的处理方式
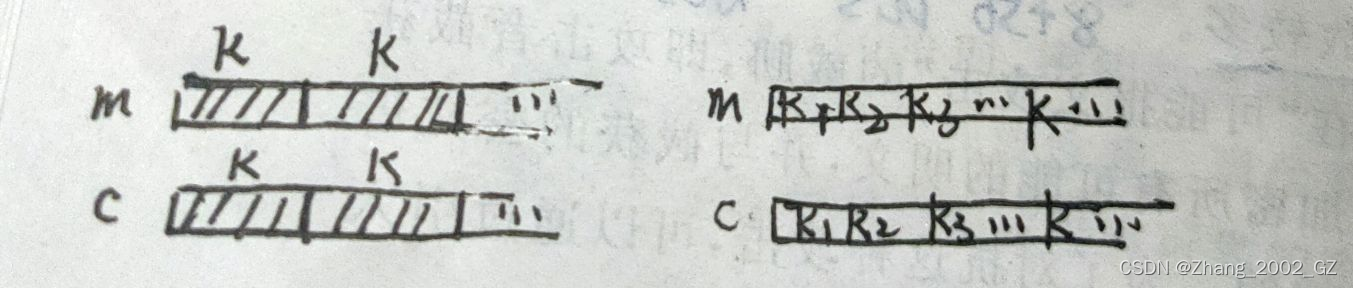
可将对称密码体制再分为分组密码和序列密码(流密码)
| 分组密码 | 序列密码(字符流) |
|---|---|
| 一个字符/1 bit处理 k足够长,不重复使用 密钥非常重要(异或) |
根据是否能进行可逆的加密变换
| 单向函数密码体制 | 双向变换密码体制 |
|---|---|
| 例子: b%m=c |
对称密码体制的优缺点
-
优点
加密、解密的处理速度快、效率高、算法安全性高
-
缺点
- 密钥分发过程复杂,说花代价高
- 密钥管理量的困难
非对称密码体制的优缺点
-
优点
- 密钥分配简单
- 系统密钥量少
- 系统开放性好(随便加入正负)
- 可以实现数字签名(私钥不可伪造性;不可否认性:因偷了或丢了造成的损失都要负责)
-
缺点
加密、解密的运算复杂、处理速度较慢,同等安全强度下,非对称密码体制的密钥位数较多
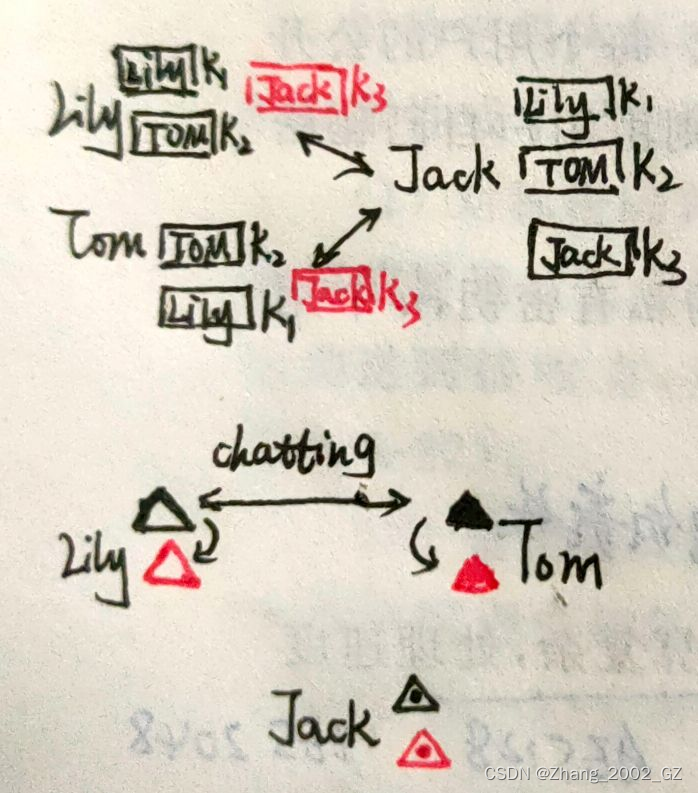
对称密码体制是每个人都有其他人的密钥,一旦加了一个人就要通知所有人人手增加一把新人的密钥。
对称密码体制每人一把公钥和私钥,用收件人的公钥加密信件,收件人只需要用自己的私钥解密即可。若增加一人只需给新人配两把公私密钥就行,不需要通知所有人


